Improved COVID-19-Models: What if ...?
Note: This is an automated translation (by DeepL) of the original german article.
The more data about COVID-19 is known, the better the spread of the virus can be understood. Since January, a team of the Vienna University of Technology and its spin-off company dwh has been working on analysing the spread of COVID-19 in Austria with the help of computer models.
A computer model developed by the simulation team over many years is used for this purpose. "It is an agent-based model, which means that we are able to simulate a very large number of virtual people on the computer and thus trace the spread of an epidemic step by step," explains Niki Popper, head of the team.
Many parameters that need to be fine-tuned
This approach has a decisive advantage: It is possible to examine certain measures in great detail and with great precision. What are the effects of a school closure? This can be investigated by not sending the simulated school children to the virtual school in the computer model. What happens if the number of leisure contacts is reduced, shops are opened, the availability of test results is accelerated? In an agent-based model, all this can be well represented.
But this advantage is also the difficult part of the method - because if you can reproduce many details, you also need to know about many different parameters, from the age structure of the population to different infection probabilities for different people in different situations. "Estimating these parameters was an important part of our work from the very beginning. We can draw on scientific literature and current studies, but as always in science, there are certain uncertainties," says Christoph Urach.
But the more data on COVID-19 is available, the better we know these parameters: The computer model has now been carefully adjusted so that the observed course of the epidemic corresponds very well with the results of the computer simulation (see Fig. 1). "The agreement is now so high that we can now estimate the necessary parameters very accurately," says Claire Rippinger. "And if you know these parameters, you can also investigate how the numbers would have developed if other measures had been taken."
The team is currently working on further simulations together with Gesundheit Österreich, MedUni Vienna and the Complexity Science Hub Vienna. This involves the analysis of further action scenarios, in particular the effects of local clusters and the effects on the reproduction number R.
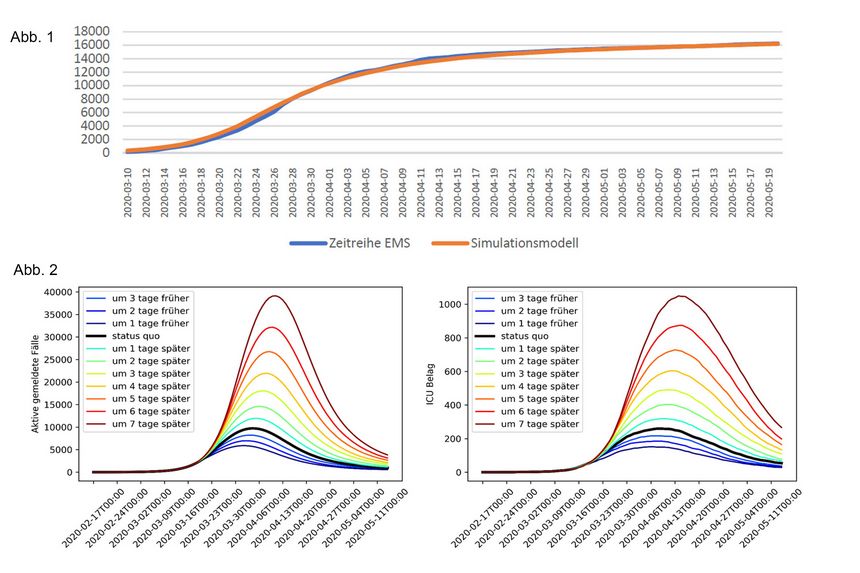
What would have happened if the measures had come later?
With the model calibrated in this way, it is now also possible to estimate how the number of infected persons would have developed if the same measures had been taken a little earlier or a little later. This shows that the "peak" of the curve, i.e. the point in time when the greatest number of people fell ill at the same time, would hardly have shifted. However, the height of this peak depends sensitively on how quickly the measures are taken: If one had waited a week longer, the number of people infected would have been about four times the number actually observed (see Fig. 2). In this case, the intensive care units of hospitals (with an ICU requirement of just over 1,000 cases) would also have reached the Austrian resource limits. "However, this study only examined what effect the postponement of the entire package of measures and the change in people's behaviour would have had. Since all these measures were introduced simultaneously in Austria, it is not possible to assess the individual measures separately in this model," says Niki Popper.
What would have happened if the measures had been withdrawn earlier?
Another model calculation (see Fig. 3) examined how the figures would have developed if the school closures, business closures or both had already been reversed on 1 April. This simulated an abrupt start, not a staggered opening - i.e. classes would have started on 1 April for all pupils without exception, and when the shops opened, both large and small shops would have reopened at the same time.
It is assumed that a large proportion of the pupils (92.4% of 0-9 year olds and 78.5% of 10-19 year olds) have an asymptomatic course of disease. For these persons it is assumed that they are infectious for an average of 7 days.
"According to our model, an earlier opening of schools or shops would have led to a renewed increase in confirmed COVID-19 cases," says Niki Popper. It is interesting to note that the opening of schools and shops (each considered on their own) have different effects: The opening of shops initially results in a higher number of reported active cases than the opening of schools, but in the longer term the two curves converge. This is due to the age-dependent probability of asymptomatic illness: it is high especially for children. Accordingly, infected children very rarely appear in the confirmed case numbers, but they can freely infect other people in their household or other surroundings, who in turn appear in the statistics with a certain time lag.
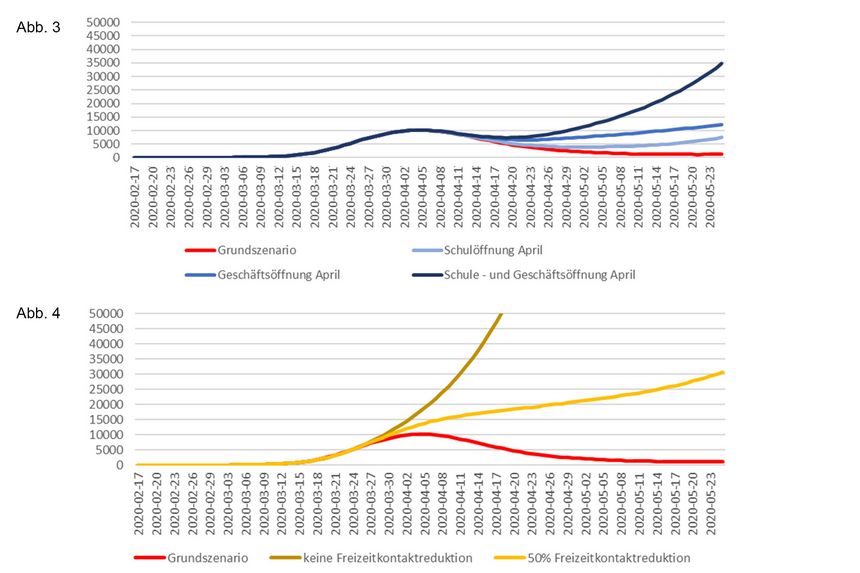
What would have happened without a reduction in leisure contact?
In the basic scenario, a reduction in leisure contact of up to 90% is assumed during the period of the initial restrictions (currently it is still about 50%). This corresponds to the analysis of mobile phone data of an Austrian provider.
Now a scenario has been simulated in which there would have been either no reduction in leisure time contact at all, or only a reduction of 50% from the beginning. However, it is assumed that hygiene measures and distance guidelines are observed.
It is shown that according to this model, the reduction of leisure contacts played a very decisive role in containing the epidemic. The closure of schools and shops alone, as well as the hygiene and distance regulations, are not sufficient to slow down the spread of the disease to a sufficient extent. Although a 50% reduction in contact during leisure time would have caused a noticeable slowdown in the spread of the disease compared to the scenario without contact reduction, the number of reported cases of the disease would not have fallen again in this way.
The significant reduction in leisure time contact was particularly important in the initial phase of the epidemic: in the meantime, the number of leisure time contacts has risen to about 50% of the normal level, but this is not necessarily a problem, because the number of cases of illness is now much lower.
Translation by DeepL, author of original Version: Florian Aigner, TU Wien